Graph analytics can be viewed in Rhumbl in two places: on a per-node level in the Info Pane, and on a map level in the Info Sidebar.
Map level metrics are metrics that give a bird's eye view of the big picture. For instance, graph density is a common map-level metric that tells you how dense a graph is in terms of edges. To see map level metrics, click on the See map statistics under the search box:
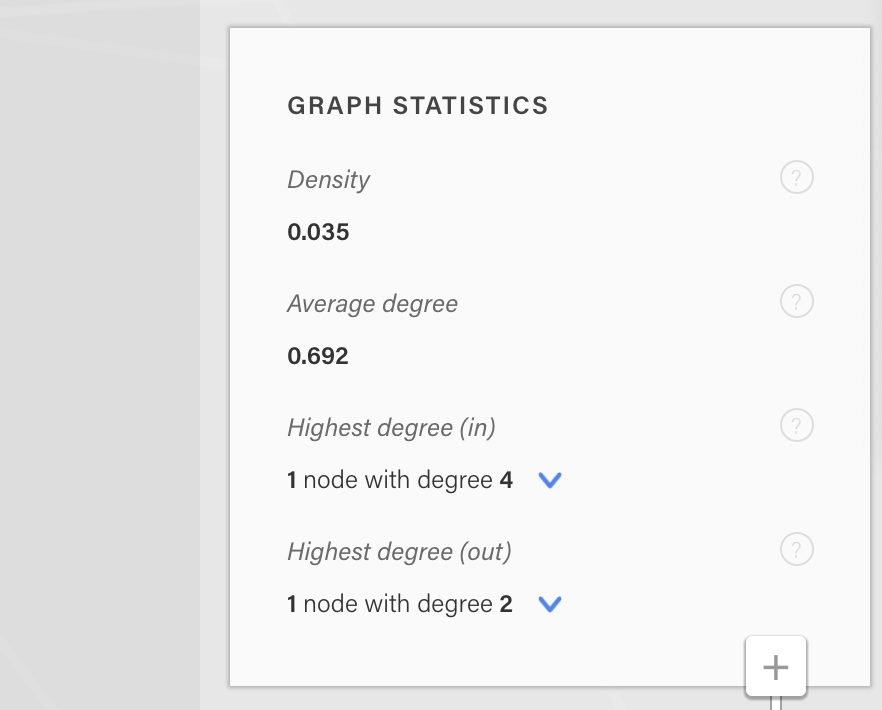
You may be already familiar with the way many of these metrics are calculated in typical graph analysis. But here, we have to be a bit more careful because Rhumbl supports multiple types of relationships and graphs that have both directed and undirected relationships. Therefore, Rhumbl calculates your map level metrics as an average across all types of edges.
One of the most common questions we get is: how do my metrics compare to the average? The answer to that is entirely dependent on the application — a network on protein-protein interactions is going to have dramatically different metrics than a network on product features.
Node level metrics are specific to each node, and can be seen by clicking on a node.

In these formulas, $E$ is the number of edges and $V$ is the number of nodes. Note that parent relationships are not counted as edges, and entities that are groups are not counted as nodes.
Density
For undirected graphs:
$$\frac{2 * E}{V (V-1)}$$For directed graphs:
$$\frac{E}{V (V-1)}$$Simple definition: The density of a graph is the ratio of the number of edges to the number of possible edges.
Why it's important: Density tells you how "connected" your entities are. Networks that are dense typically have a lot of redundancy — if you break a link to a node, it's likely it's still connected via another path.
Average degree
Simple definition: The average number of incoming or outgoing edges per node, calculated as the number of edges divided by the number of nodes.
Why it's important: You can use this number as a comparison against nodes with really high in- or out-degrees. Note that the average incoming and outgoing degree is identical.
Highest degree (in/out)
Simple definition: The node with the highest number of edges (incoming / outgoing).
Why it's important:The highest degree nodes are ones that are worth paying attention to — this could be a hot spot, e.g. a person that everybody knows, a feature that everything depends on, etc.
More coming soon! We are actively working on updating these docs as well as releasing more graph metrics.